MK 4.6.2003 Terme.mcd
Terme
Def.:
Mit Hilfe zulässiger Rechenoperationen
gebildete Ausdrücke heißen Terme. Ein Term kann aus
Konstanten, Formvariablen (Parametern) und
Variablen gebildet werden.
Variable sind immer variabel und meist mit
Buchstaben vom Ende des Alphabets bezeichnet.
Parameter sind für eine bestimmte Betrachtung
konstant und ändern ihren Wert nur von Fall
zu Fall. Für Parameter werden Buchstaben vom
Anfang des Alphabets verwendet.
Bsp.:
Zwei Konstante: 2 und 1
Eine Variable: x
Zwei Operationen: * und +
Zwei Konstante: 8 und 9
Keine Variable
Eine Operation: *
Drei Konstante: 2, 5 und 14
Eine Variable: x
Ein Parameter: a
Vier Operationen: / ,+, * und +
Keine Konstanten
Eine Variable: x
Zwei Parameter: a und b
Vier Operationen:
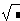, *, ^2 und -
Def.:
Die Menge, aus der Einsetzungen für die
Variablen vorgegeben werden heißt Grundmenge G.
(Bei uns Standard: R)
Die Menge aller Elemente, für die ein Term
definiert ist, heißt Definitionsmenge D.
Also: Bedingungen an Variable bilden die
Definitionsmenge. Bedingungen an Parameter nennt man
Voraussetzungen. Dafür benennt man nicht
extra eine Menge.
Der Begriff Lösungsmenge ist nicht speziell
an Terme geknüpft. Eine Lösungsmenge setzt eine
mathematische Aussage voraus (meist eine
Gleichung) und bezeichnet die Menge derjenigen Elemente,
die die Aussage wahr werden lassen.
Bsp.:
Sei G = R und
Hier ist D = R+0
und Voraussetzung
wäre
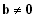
Aufgabe: Bestimme in der Grundmenge R die
Definitionsmenge der folgenden Terme
Lösungen:
T1:
D = R \ {
}
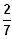T2:
D = R0+
T3:
=>
D = ] -1 ;
[
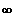T4:
=>
D = R \ { 2; 3 }
T5:
=>
D = R \ {
;
}
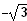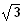T6:
=>
D = R \ [ -5; 5 ]
T7:
=>
=> -7 , 2 sind verboten
n. unten geöffnete Parabel => ] -4 ; 1 [
ist definiert
=>
0 ist verboten
insgesamt:
D = ]
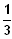; 1[
