MK 4.6.2003 LineareAbhaengigkeit.mcd
Lineare Abhängigkeit
Lineare Abhängigkeit oder Unabhängigkeit
von Vektoren.
Def.:
Gilt für die Gleichung
zwingend alle
,
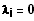so sind die Vektoren
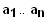
linear unabhängig. Gibt es jedoch mindestens ein
,
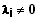so sind sie linear abhängig.
Satz:
In einer Ebene gibt es maximal zwei linear
unabhängige Vektoren.
Im Raum gibt es maximal drei linear unabhängige
Vektoren.
(Drei Vektoren in der Ebene sind also immer linear
abhängig, genauso wie vier im Raum.)
Zwei Vektoren sind linear abhängig, wenn sie
parallel sind und umgekehrt.
Drei Vektoren sind linear abhängig, wenn sie in
einer Ebene liegen (komplanar sind) und umgekehrt.
Beweise:
In einer Ebene gibt es maximal zwei linear
unabhängige Vektoren.
Beweis: Man kann immer folgende Konstruktion
durchführen: Der Vektor a ist Diagonale eines
Parallelogramms, dessen Seiten parallel zu den
Vektoren b und c sind. Also muss a
eine
Linearkombination aus b
und c sein:
,
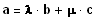
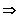
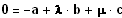da
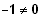ist, sind die drei Vektoren linear abhängig.
Zwei Vektoren sind linear abhängig, wenn sie
parallel sind und umgekehrt.
Voraussetzung:
mit
,
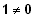also linear abhängig.
Voraussetzung:
mit einem
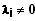
sei hier
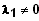
also parallel
Im Raum gibt es maximal drei linear unabhängige
Vektoren.
Beweis: Man kann immer folgende Konstruktion
durchführen: Der Vektor a ist Raumdiagonale eines
Parallelvielflachs (Spat), dessen Seiten parallel
zu den Vektoren b, c und d sind. Also muss a
eine
Linearkombination aus b,
c und d sein:
,
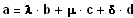
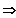
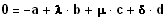da
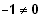ist, sind die drei Vektoren linear abhängig.
Drei Vektoren sind linear abhängig, wenn sie in
einer Ebene liegen und umgekehrt.
Voraussetzung:
"Liegen in einer Ebene", siehe Beweis "maximal
zwei linear unabhängige Vektoren"
mit
,
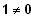also linear abhängig.
Voraussetzung:
mit einem
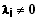
sei hier
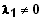
also liegen sie in einer Ebene
Def.:
Eine endliche Menge von linear unabhängigen
Vektoren, aus den (durch Linearkombination) der Vektorraum V erzeugt
werden kann, heißt Basis
von V.
Die Anzahl der Basisvektoren eines Vektorraums V,
heißt Dimension
von V.
Folgerung:
Eine Ebene besitzt die Dimension 2, jeder Vektor
der Ebene läßt sich als Linearkombination zweier linear unabhängiger
Vektoren darstellen.
Der Raum besitzt die Dimension 3, jeder Vektor des
Raumes läßt sich als Linearkombination dreier linear unabhängiger
Vektoren darstellen.
