RS 24.2.2005 Erwartungswert_Varianz_i.mcd
Erwartungswert, Varianz, Standardabweichung
4) Erwartungswert
Bei jedem Glücksspiel interessieren den Spieler vor allem die Gewinnchancen.
1. Beispiel: Setzen auf 1. Dutzend beim Roulett
Ein Spieler setzt auf 1. Dutzend. Trifft die Kugel eine der Zahlen 1 - 12, so wird der dreifache Einsatz ausbezahlt, der Reingewinn ist also der doppelte Einsatz. Kommt eine andere der 37 Zahlen, so geht der Einsatz verloren.
Zufallsgröße
X
Wahrscheinlichkeitsverteilung
 P
Reingewinn
Der durchschnittliche Gewinn (Erwartungswert) errechnet sich wie folgt:
Der durchschnittliche Gewinn (Erwartungswert) ist negativ, d. h. langfristig ist mit einem Verlust zu rechnen oder anders gesagt:
 Die Bank gewinnt immer.
Definition
 Der Erwartungswert m = E(X) einer Zufallsgröße X mit der Wertemenge W = { x0, x1, x2, ... , xN } errechnet sich wie folgt:
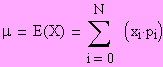
Für obiges Beispiel folgt:
Merke: Der Erwartungswert ist der Mittelwert der Statistik.
Merke: Ein Glücksspiel mit dem Erwatungswert m = 0 wird als fair bezeichnet.
2. Beispiel: Berechnung des Notendurchschnitts einer Klasse
Notenverteilung einer Klasse
Klassenstärke
Notendurchschnitt:
oder
Die Noten sind hier die Zufallsgrößen
Anzahl/S
ist hier die Wahrscheinlichkeit, eine bestimmte Note zu erhalten,
 z. B. P(Note 1) = 3/30 = 0,1.
5) Varianz und Standardabweichung
Für den Erwartungswert gilt bekanntlich:
Im Folgenden:
Die Varianz einer Zufallsgröße X ist ein Maß für die Streuung der Zufallsgröße X um den Erwartungswert E(X) = m.
- Berechnet wird zunächst der quadrierte Abstand der Zufallsgröße Xi vom Erwartungswert m: (X - m )2
 - Dieser Abstand wird noch mit der Wahrscheinlichkeit für das Auftreten der Zufallsgröße Xi multipliziert (gewichtet): (X - m )2 *P(xi)
 - Zum Schluß werden alle diese Werte aufaddiert.
Die Varianz errechnet sich somit wie folgt:
Die Varianz kann somit auch als Erwartungswert der neuen Zufallsgröße
 Y = (X - m )2 aufgefasst werden.
Für die Standardabweichung gilt:
Herleitung der Verschiebungsformel
oder
Verschiebungsformel zur Berechnung der Varianz
1. Beispiel: "1. Dutzend beim Roulett"
Zufallsgröße X beschreibt den Reingewinn
Wahrscheinlichkeitsverteilung von X
Erwartungswert
Varianz
Standardabweichung
Eine häufige Frage lautet:
 Mit welcher Wahrscheinlichkeit nimmt die Zufallsgröße X Werte in einer s-Umgebung des Erwartungswertes m an. Die mathematische Übersetzung lautet:
Mit einer Wahrscheinlichkeit von 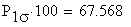% liegen die Werte dieser Zufalsgröße X in einer einfachen Standardumgebung des Erwartungswertes.
Wie man deutlich sieht, liegt innerhalb einer einfachen Standardabweichung vom Erwartungswert nur die Zufallsgröße X = -1, die den Verlust des Einsatzes beschreibt. Die Wahrscheinlichkeit 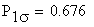stimmt deshalb auch mit der Verlustwahrscheinlichkeit überein.
2. Beispiel: "Setzen auf genau eine Zahl beim Roulett"
Setzt ein Spieler beim Roulett-Spiel auf genau eine Zahl, z. B. die Zahl 7, so erhält er bei Erscheinen dieser Zahl den 36-fachen Einsatz ausbezahlt, d. h. der Reingewinn ist der 35-fache Einsatz.
Zufallsgröße X beschreibt den Reingewinn
Wahrscheinlichkeitsverteilung der Zufallsgröße X
Erwartungswert
Varianz
Standardabweichung
Eine häufige Frage lautet:
 Mit welcher Wahrscheinlichkeit nimmt die Zufallsgröße X Werte in einer s-Umgebung des Erwartungswertes m an. Die mathematische Übersetzung lautet:
Mit einer Wahrscheinlichkeit von 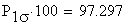% liegen die Werte dieser Zufalsgröße X in einer einfachen Standardumgebung des Erwartungswertes.
Wie man deutlich sieht, liegt innerhalb einer einfachen Standardabweichung vom Erwartungswert nur die Zufallsgröße X = -1, die den Verlust des Einsatzes beschreibt. Die Wahrscheinlichkeit 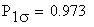stimmt deshalb auch mit der Verlustwahrscheinlichkeit überein.
Die Zufallsgröße X = 35, die den Gewinn kennzeichnet, ist weit außerhalb der einfachen Standardabweichung vom Erwartungswert.
Beim 1. Beispiel, "Setzen auf 1. Dutzend" ist die Zufallsgröße X = 2 (Gewinn) näher an der einfachen Standardabweichung vom Erwartungswert.
Die Standardabweichung bei "Setzen auf 1. Dutzend" ist auch viel kleiner als beim "Setzen auf genau eine Zahl".
Faustregel:
 Eine hohe Varianz und damit eine große Standardabweichung weisen auf ein hohes Spielerrisiko hin.
3. Beispiel
Gegeben sei eine Zufallsgröße X die folgende Werte annimmt:
Zu den einzelnen Werten der Zufallsgröße X gehören folgende Wahrscheinlichkeiten:
Erwartungswert
Varianz
Standardabweichung
Mit welcher Wahrscheinlichkeit nimmt diesmal die Zufallsgröße X Werte in einer s-Umgebung des Erwartungswertes m an.
Die mathematische Übersetzung lautet wieder:
Mit einer Wahrscheinlichkeit von 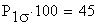% liegen die Werte dieser Zufalsgröße X in einer einfachen Standardumgebung des Erwartungswertes.
4. Beispiel: Notenverteilung in einer Klasse
Notenverteilung einer Klasse
Klassenstärke
Wie oben bereits gezeigt, gilt:
Die Noten sind hier die Zufallsgrößen
Anzahl/S
ist hier die Wahrscheinlichkeit, eine bestimmte Note zu erhalten,
 z. B. P(Note 1) = 3/30 = 0,1.
Der Erwartungswert stimmt selbstverständlich mit dem Notendurchschnitt überein:
Erwartungswert
Die Varianz errechnet sich wie folgt:
Für die Standardabweichung gilt:
Mit welcher Wahrscheinlichkeit nimmt die Zufallsgröße X Werte in einer s-Umgebung des Erwartungswertes m an. Die mathematische Übersetzung lautet:
Die Noten 3, 4 und 5 liegen in diesem Fall in einer Standardumgebung des Erwartungswertes,
d. h. des Notendurchschnittes.
Mit einer Wahrscheinlichkeit von 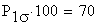% liegen die Werte dieser Zufalsgröße X in einer einfachen Standardumgebung des Erwartungswertes.
Impressum · Datenschutz