RS 24.2.2005 Verteilungsfunktion.mcd
Verteilungsfunktion
3) Verteilungsfunktion
1. Beispiel
Ein Spieler einer Eishockeymannschaft wird verletzt.
Erfahrungsgemäß dauert die Heilung zwischen 3 und 8 Tagen.
Die Zufallsgröße X kennzeichne die Anzahl der Tage, die
Wahrscheinlichkeit P(X = xi) gibt an, mit welcher
Wahrscheinlichkeit der Spieler an einem bestimmten Tag gesund sein wird.
Den Trainer interessiert die Frage, wie sicher dieser Spieler
am entscheidenden Spiel in 7 Tagen teilnehmen kann. Die Antwort ist
leicht einzusehen:
=
Mit einer Wahrscheinlichkeit von 95% ist der verletzte
Spieler erfahrungsgemäß am 7. Tag wieder gesund.
Diese hier notwendige Addition von Wahrscheinlichkeiten wird
mit Hilfe der Verteilungsfunktion beschrieben.
Definition:
Für die Verteilungsfunktion
gilt:
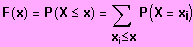D(F) = IR
Aus dieser Definition lassen sich sofort einige Eigenschaften
der Verteilungsfunktion F ableiten:
a)
Die Zufallsgröße X nimmt nur endliche
Werte an. Darunter ist ein Wert der absolut
kleinste Wert Xmin. Die Wahrscheinlichkeit
dafür, dass die Zufallsgröße X einen
Wert annimmt, der kleiner als Xmin
ist, ist für alle reellen Zahlen x<Xmin gleich Null.
b)
Die Summe aller Wahrscheinlichkeiten ist eben gleich 1.
c)
F(x) ist monoton wachsend.
Es werden ja nur positive Werte dazuaddiert.
d)
Die Eigenschaften d) - f) lassen sich unmittelbar
aus der Definition von F(x) erschließen.
e)
f)
Beschreibung des Funktionsterms am
Beispiel des Eishockeyspielers
Anzahl der Tage im Krankenstand
Wahrscheinlichkeit einer Genesung
Tabelle der Verteilungsfunktion F (hier "Vert1"):
oder
oder
Graph einer Verteilungsfunktion
2. Beispiel
Gegeben sei eine Zufallsgröße X die folgende Werte
annimmt:
Zu den einzelnen Werten der Zufallsgröße X
gehören folgende Wahrscheinlichkeiten:
Tabelle der Verteilungsfunktion F:
oder
oder
Graph dieser Verteilungsfunktion
Berechnung
der Wahrscheinlichkeitsverteilung einer Zufallsgröße X aus
den Werten einer Verteilungsfunktion
Aus der oben definierten Matrix "Vert1" entnehme
ich die charakteristischen Daten der Verteilungsfunktion Ft:
Berechnung des Vektors der
Wahrscheinlichkeitsverteilung:
Ergebnis aus den Werten der Verteilungsfunktion
Ursprünglich gegebene
Wahrscheinlichkeitsverteilung
Graph
der Verteilungsfunktion als abschnittsweise definierte Funktion
Gegebene Zufallsgröße
Berechnung
von Wahrscheinlichkeiten mit Hilfe der Verteilungsfunktion
Die dunkle blaue Strecke veranschaulicht die
berechnete Wahrscheinlichkeit.
Die dunkle blaue Strecke veranschaulicht die
berechnete Wahrscheinlichkeit.
Die dunkle blaue Strecke veranschaulicht die
berechnete Wahrscheinlichkeit.
