GS - 24.08.04 - abl_04_ersteAbl.mcd
Die erste Ableitung
- Monotonieeigenschaft -
1.
Horizontale Tangenten:
Beispiel: Gegeben sind
Parabel 1:
Parabel 2:
bzw.
bzw.
Ändern des Kurvenpunktes
Ergebnis:
Parabeln haben im Scheitel S(x0
/ f(x0)
eine horizontale Tangente, die Steigung ist also im ent-
sprechenden Kurvenpunkt S Null. Also:
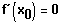
Das ist die Nullstelle der 1. Ableitung.
Ableitung:
Ableitung:
Berechnung der Nullstelle:
Berechnung der Nullstelle:
2.
Die Ableitungsfunktion:
Definition:
Unter der "Ableitungsfunktion" (kurz "Ableitung") einer Funktion
f versteht man die Funktion f´, welche jeder Zahl x0 die Steigung der Tangente im Punkt
P(x0/f(x0))
des Graphen von zuordnet: (
f´: IR --> IR
x I-->
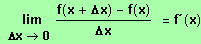
Bezeichnung: Die
Ableitung f´(x) wird im Folgenden auch
mit fx(x)
bezeichnet
3.
Die Graphen von Funktion und Ableitungsfunktion:
Beispiel: Gegeben sind
Es
gilt: Die
Ableitung einer
ganzrationalen Funktion ist
selbst wieder eine ganzrationale Funktion, die Ableitungsfunktion
ist also differenzierbar.
Folgerungen:
Aus dem Verlauf des Graphen der Ableitungsfunktion
f´(x) kann man unmittelbar die Steigung m = f´(x0)
in einem beliebigen Punkt P( x0
/ f(x0)
) ablesen.
Satz: Notwendige
Bedingung für ein relatives Extremum (FS Seite
63 / G4b)
In den Nullstellen der Ableitungsfunktion hat die
Funktion eine horizontale
Tangente: f´(x) = 0
4.
Monotonie:
Definition: (FS
Seite 64 / G3)
Ist f´(x)
> 0, so
ist der Graph der Funktion Gf streng
monoton steigend (smost).
Ist f´(x)
< 0, so
ist der Graph der Funktion Gf streng
monoton fallend (smofa).
Zur Erinnerung:
f´(x) > 0
f´(x) > 0
rel. Maximum
smost
smofa
f´(x) < 0
smofa
smost
rel. Minimum
5.
Art des Extremums
über die Monotonie:
Satz: Hinreichende
Bedingung für ein relatives Extremum (FS Seite
63 / G4a)
Wechselt die Ableitungsfunktion f´(x) an der
Stelle x0 das
Vorzeichen von positiv nach negativ, so hat
die Funktion f an der Stelle x0 ein relatives
Maximum.
Wechselt die Ableitungsfunktion f´(x) an der
Stelle x0 das
Vorzeichen von negativ nach positiv , so hat
die Funktion f an der Stelle x0 ein relatives
Minimum.
Bemerkung:
Dieses Kriterium verlangt nicht die notwendige
Bedingung der horizontalen Tangente. Es ist also auch anwendbar auf
nicht differenzierbare Funktionen, z.B. bei einem Extremum auf der
Nahtstelle.
6.
Erweiterte Formulierung
der Monotonie:
Maximale
Monotoniebereiche:
Gilt f´(x0)
= 0 für einzelne Stellen x0, so ist der Graph der
Funktion dennoch streng monoton steigend bzw. streng monoton fallend.
Der
Graph der Ableitung hat dann eine einfache oder eine zweifache
Nullstelle.
Beispiel:
Die Ableitung f5´(x) besitzt die
zweifache
Nullstelle
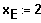
Die Ableitung f6´(x) besitzt die
einfache
Nullstelle
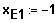 und
und
die zweifache
Nullstelle
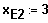
Monotonie:
Gf3 ist streng monoton steigend
für alle x.
Monotonie:
Gf4 ist streng monoton steigend
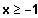 .
.